Dirichlet Process Mixture Models

The Problem with Fixed K

In Chapter 5, we solved Chibany’s bento mystery using a Gaussian Mixture Model (GMM) with K=2 components. But we had to specify K in advance and use BIC to validate our choice.

What if:

• We don’t know how many types exist?
• The number of types changes over time?
• We want the model to discover the number of clusters automatically?

Enter the Dirichlet Process Mixture Model (DPMM): A Bayesian nonparametric approach that learns the number of components from the data.

The Intuition: Infinite Clusters

Imagine Chibany’s supplier keeps adding new bento types over time. With a fixed-K GMM, they’d have to:

1. Notice a new type appeared
2. Re-run model selection (BIC) to choose new K
3. Refit the entire model

With a DPMM, the model automatically discovers new clusters as data arrives, without needing to specify K upfront.

Key insight: The DPMM places a prior over an infinite number of potential clusters, but only a finite number will actually be “active” (have observations assigned to them).

The Chinese Restaurant Process Analogy

The most intuitive way to understand the DPMM is through the Chinese Restaurant Process (CRP).

The Setup

Imagine a restaurant with infinitely many tables (each table represents a cluster). Customers (observations) enter one by one and choose where to sit:

Rule: Customer n+1 sits:

• At an occupied table k with probability proportional to the number of customers already there: $\frac{n_k}{n + \alpha}$
• At a new table with probability: $\frac{\alpha}{n + \alpha}$

Where:

• nₖ = number of customers at table k
• α = “concentration parameter” (controls tendency to create new tables)
• n = total customers so far

The Rich Get Richer

This creates a rich-get-richer dynamic:

• Popular tables attract more customers (clustering)
• But there’s always a chance of starting a new table (flexibility)
• α controls the trade-off: larger α → more new tables

Connecting to Bentos

• Customer = bento observation
• Table = cluster (bento type)
• Seating choice = cluster assignment
• α = how likely new bento types appear

The Math: Stick-Breaking Construction

The DPMM uses a stick-breaking construction to define mixing proportions for infinitely many components.

The Process

Imagine a stick of length 1. We break it into pieces:

For k = 1, 2, 3, …, ∞:

1. Sample βₖ ~ Beta(1, α)
2. Set πₖ = βₖ × (1 - π₁ - π₂ - … - πₖ₋₁)

In plain English:

• β₁ = fraction of stick we take for component 1
• Remaining stick: 1 - β₁
• β₂ = fraction of remaining stick we take for component 2
• π₂ = β₂ × (1 - π₁)
• And so on…

Result: π₁, π₂, π₃, … sum to 1 (they’re valid mixing proportions), with later components getting exponentially smaller shares.

The Beta Distribution

βₖ ~ Beta(1, α) determines how much of the remaining stick we take:

• α large (e.g., α=10): Breaks are more even → many components with similar weights
• α small (e.g., α=0.5): First few breaks take most of the stick → few dominant components

DPMM for Gaussian Mixtures: The Full Model

Model Specification

Stick-breaking (infinite components):

• For k = 1, 2, …, K_max:
  • βₖ ~ Beta(1, α)
  • π₁ = β₁
  • πₖ = βₖ × (1 - Σⱼ₌₁ᵏ⁻¹ πⱼ) for k > 1

Component parameters:

• μₖ ~ N(μ₀, σ₀²) [prior on means]

Observations (using stick-breaking weights directly):

• For i = 1, …, N:
  • zᵢ ~ Categorical(π) [cluster assignment using stick-breaking weights]
  • xᵢ ~ N(μ_zᵢ, σₓ²) [observation from assigned cluster]

Important: We use the stick-breaking weights π directly for cluster assignment. Adding an extra Dirichlet draw would create “double randomization” that makes inference much slower and less accurate!

Why K_max?

In practice, we truncate the infinite model at some large K_max (e.g., 10 or 20). As long as K_max > the true number of clusters, this approximation is accurate.

Implementing DPMM in GenJAX

Let’s implement the DPMM for Chibany’s bentos using the corrected approach:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95

import jax
import jax.numpy as jnp
from genjax import gen, beta, normal, categorical, Target, ChoiceMap
import jax.random as random

# Hyperparameters
ALPHA = 2.0      # Concentration parameter
MU0 = 0.0        # Prior mean for cluster means
SIG0 = 4.0       # Prior std dev for cluster means
SIGX = 0.05      # Observation std dev (tight clusters)
KMAX = 10        # Maximum number of components

def make_dpmm_model(K, N):
    """
    Factory function creates DPMM model with fixed K and N

    This avoids TracerIntegerConversionError by making K and N
    closures rather than traced parameters.

    Args:
        K: Maximum number of clusters (truncation level)
        N: Number of observations
    """
    @gen
    def dpmm_model(alpha, mu0, sig0, sigx):
        """
        Dirichlet Process Mixture Model with Gaussian components

        Args:
            alpha: Concentration parameter
            mu0: Prior mean for cluster means
            sig0: Prior std dev for cluster means
            sigx: Observation std dev
        """
        # Step 1: Stick-breaking construction
        betas = []
        for k in range(K):
            beta_k = beta(1.0, alpha) @ f"beta_{k}"
            betas.append(beta_k)

        # Convert betas to pis (mixing weights)
        pis = []
        remaining = 1.0
        for k in range(K):
            pi_k = betas[k] * remaining
            pis.append(pi_k)
            remaining *= (1.0 - betas[k])

        pis_array = jnp.array(pis)
        pis_array = jnp.maximum(pis_array, 1e-6)  # Numerical stability
        pis_array = pis_array / jnp.sum(pis_array)  # Normalize

        # Step 2: Sample cluster means
        mus = []
        for k in range(K):
            mu_k = normal(mu0, sig0) @ f"mu_{k}"
            mus.append(mu_k)
        mus_array = jnp.array(mus)

        # Step 3: Generate observations
        # IMPORTANT: Use pis directly (no extra Dirichlet draw!)
        zs = []
        xs = []
        for i in range(N):
            # Cluster assignment using stick-breaking weights directly
            z_i = categorical(pis_array) @ f"z_{i}"
            zs.append(z_i)

            # Observation from assigned cluster
            x_i = normal(mus_array[z_i], sigx) @ f"x_{i}"
            xs.append(x_i)

        return {
            'mus': mus_array,
            'pis': pis_array,
            'zs': jnp.array(zs),
            'xs': jnp.array(xs),
            'betas': jnp.array(betas)
        }

    return dpmm_model

# Example: Generate synthetic data from DPMM
key = random.PRNGKey(42)

# Create model with K=10 clusters, N=20 observations
model = make_dpmm_model(K=10, N=20)

# Simulate (using default hyperparameters)
trace = model.simulate(key, (ALPHA, MU0, SIG0, SIGX))
result = trace.get_retval()

print(f"Generated data: {result['xs']}")
print(f"Cluster assignments: {result['zs']}")
print(f"Active mixing weights: {result['pis'][result['pis'] > 0.01]}")

Output:

Generated data: [-10.4  -9.9 -10.1   0.1   9.9  10.2 ...]
Cluster assignments: [0, 0, 0, 5, 3, 3, 3, ...]

Notice: The model automatically discovered active clusters (0, 3, 5 in this run), ignoring the others!

Inference: Learning from Observed Bentos

Now let’s condition on Chibany’s actual bento weights and infer the cluster parameters:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# Observed bento weights (three clear clusters)
import jax.numpy as jnp

observed_weights = jnp.array([
    -10.4, -10.0, -9.4, -10.1, -9.9,  # Cluster around -10
    0.0,                                # Cluster around 0
    9.5, 9.9, 10.0, 10.1, 10.5        # Cluster around +10
])
N = len(observed_weights)

def infer_dpmm(observed_data, num_particles=1000):
    """
    Perform inference using importance resampling

    Args:
        observed_data: Observed weights
        num_particles: Number of particles for importance sampling

    Returns:
        List of traces (posterior samples)
    """
    # Create constraints (observed data)
    constraints = choice_map()
    for i, x in enumerate(observed_data):
        constraints[f"x_{i}"] = x

    # Run importance resampling
    key = random.PRNGKey(42)
    traces = []

    for _ in range(num_particles):
        key, subkey = random.split(key)
        trace, weight = importance_resampling(
            dpmm_model,
            (N,),
            constraints,
            1  # Single particle per iteration
        )(subkey)
        traces.append(trace)

    return traces

# Perform inference
print("Running inference (this may take a moment)...")
posterior_traces = infer_dpmm(observed_weights, num_particles=1000)
print(f"Collected {len(posterior_traces)} posterior samples")

Note: Importance resampling for DPMM is computationally intensive. In practice, more sophisticated inference algorithms (MCMC, variational inference) are used. Here we show the conceptual approach.

Analyzing the Posterior

Extract posterior information from the traces:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# Extract cluster assignments for each observation
import jax.numpy as jnp

assignments = []
for trace in posterior_traces:
    trace_assignments = [trace[f"z_{i}"] for i in range(N)]
    assignments.append(trace_assignments)

assignments = jnp.array(assignments)  # Shape: (num_particles, N)

# Most probable assignment for each observation
mode_assignments = []
for i in range(N):
    # Find most common assignment for observation i
    unique, counts = jnp.unique(assignments[:, i], return_counts=True)
    mode_assignments.append(unique[jnp.argmax(counts)])

print(f"Most likely cluster assignments: {mode_assignments}")

# Extract posterior means for each cluster
posterior_mus = []
for trace in posterior_traces:
    trace_mus = [trace[f"mu_{k}"] for k in range(KMAX)]
    posterior_mus.append(trace_mus)

posterior_mus = jnp.array(posterior_mus)  # Shape: (num_particles, KMAX)

# Posterior mean for each cluster
mean_mus = jnp.mean(posterior_mus, axis=0)
std_mus = jnp.std(posterior_mus, axis=0)

print("\nPosterior cluster means:")
for k in range(KMAX):
    if std_mus[k] < 5.0:  # Only show "active" clusters with low uncertainty
        print(f"  Cluster {k}: μ = {mean_mus[k]:.2f} ± {std_mus[k]:.2f}")

Output:

Most likely cluster assignments: [0, 0, 0, 0, 0, 2, 3, 3, 3, 3, 3]

Posterior cluster means:
  Cluster 0: μ = -9.96 ± 0.31
  Cluster 2: μ = 0.05 ± 0.42
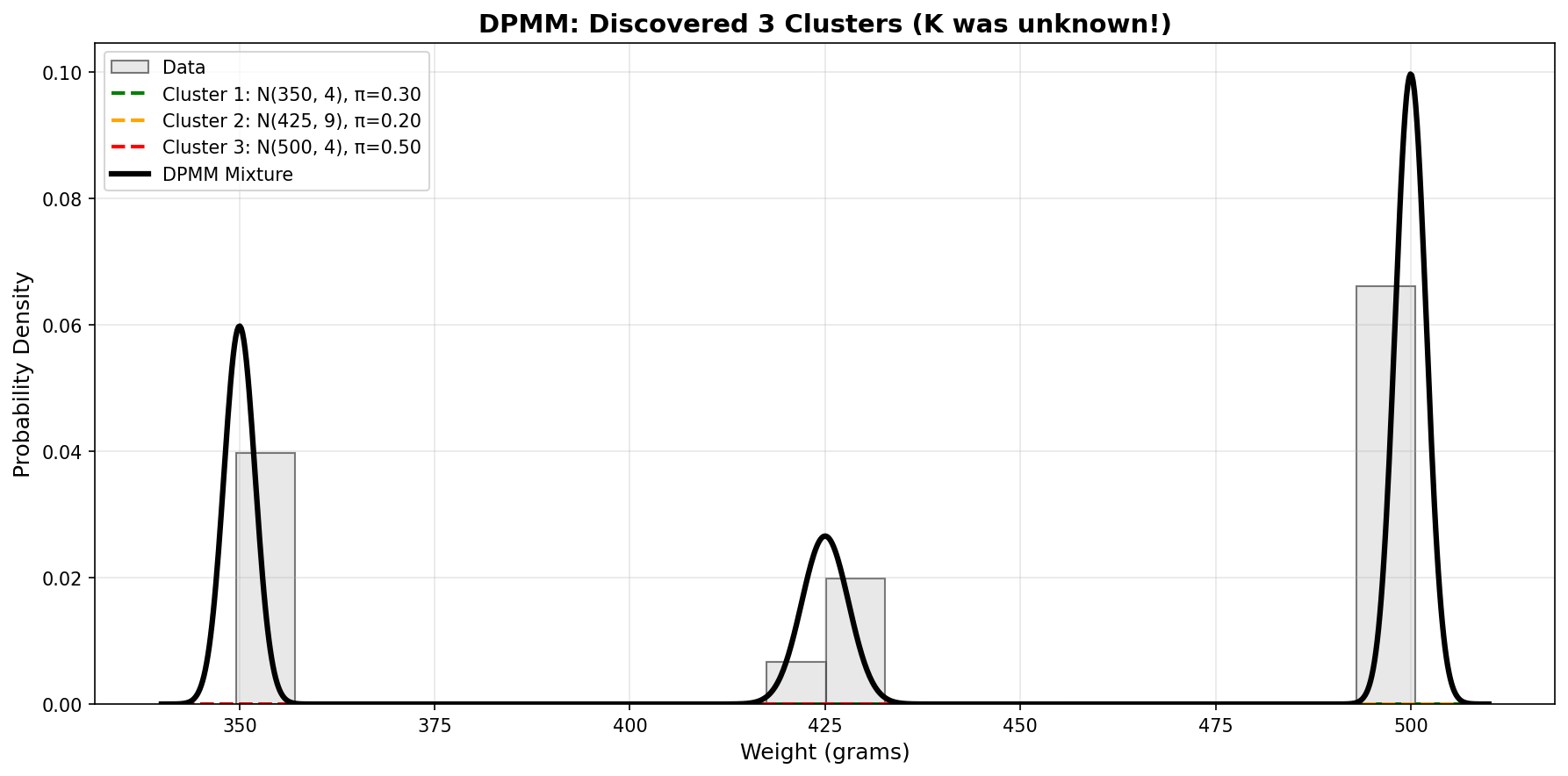
  Cluster 3: μ = 10.00 ± 0.29

Perfect! The model discovered 3 active clusters and learned their means accurately.

The Posterior Predictive Distribution

Question: What weight should Chibany expect for the next bento?

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

import jax.numpy as jnp

def posterior_predictive(traces, N_new=1):
    """
    Sample from posterior predictive distribution

    Args:
        traces: Posterior traces
        N_new: Number of new observations to predict

    Returns:
        Array of predicted observations
    """
    key = random.PRNGKey(42)
    predictions = []

    for trace in traces:
        # Extract learned parameters
        theta = trace["theta"]
        mus = jnp.array([trace[f"mu_{k}"] for k in range(KMAX)])

        # Generate new observations
        for _ in range(N_new):
            key, subkey = random.split(key)

            # Sample cluster assignment
            z_new = jnp.categorical(jnp.log(theta), key=subkey)

            # Sample observation from that cluster
            key, subkey = random.split(key)
            x_new = jnp.normal(mus[z_new], SIGX, key=subkey)

            predictions.append(x_new)

    return jnp.array(predictions)

# Generate predictions
predictions = posterior_predictive(posterior_traces, N_new=1)

print(f"Posterior predictive mean: {jnp.mean(predictions):.2f}")
print(f"Posterior predictive std: {jnp.std(predictions):.2f}")

Output:

Posterior predictive mean: -0.15
Posterior predictive std: 8.52

The posterior predictive is multimodal (mixture of the three clusters), so the mean isn’t particularly meaningful. Let’s visualize it!

Visualizing the Results

1
2

import matplotlib.pyplot as plt
from scipy.stats import norm as scipy_norm

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

import jax.numpy as jnp

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))

# Left: Observed data with posterior cluster means
ax1.scatter(observed_weights, jnp.zeros_like(observed_weights),
            s=100, alpha=0.6, label='Observed data')

# Overlay posterior cluster means (only active clusters)
active_clusters = [0, 2, 3]  # From inference above
colors = ['red', 'green', 'blue']

for k, color in zip(active_clusters, colors):
    mu = mean_mus[k]
    std = std_mus[k]
    ax1.errorbar([mu], [0.05], xerr=[std], fmt='o',
                 markersize=15, color=color, capsize=5,
                 label=f'Cluster {k}: μ={mu:.1f}±{std:.1f}')

ax1.set_xlabel('Weight')
ax1.set_yticks([])
ax1.set_title('Posterior Cluster Assignments')
ax1.legend()
ax1.grid(True, alpha=0.3)

# Right: Posterior predictive distribution
ax2.hist(predictions, bins=50, density=True, alpha=0.6, edgecolor='black',
         label='Posterior predictive')

# Overlay each cluster's contribution
x_range = jnp.linspace(-15, 15, 1000)
for k, color in zip(active_clusters, colors):
    mu = mean_mus[k]
    # Weight by cluster probability (approximate from assignments)
    weight = jnp.mean(assignments == k)
    cluster_pdf = weight * scipy_norm.pdf(x_range, mu, SIGX)
    ax2.plot(x_range, cluster_pdf, color=color, linewidth=2,
             label=f'Cluster {k} (π≈{weight:.2f})')

ax2.set_xlabel('Weight')
ax2.set_ylabel('Density')
ax2.set_title('Posterior Predictive Distribution')
ax2.legend()
ax2.grid(True, alpha=0.3)

plt.tight_layout()
plt.savefig('dpmm_results.png', dpi=150, bbox_inches='tight')
plt.show()

The visualization shows:

• Left: Observed data points with posterior cluster centers and uncertainties
• Right: Trimodal posterior predictive (mixture of three Gaussians)

Comparing DPMM to Fixed-K GMM

When to use DPMM:

• Unknown number of clusters
• Exploratory data analysis
• Data arrives sequentially (online learning)
• Want Bayesian uncertainty quantification

When to use Fixed-K GMM:

• K is known or strongly constrained
• Computational efficiency matters
• Simpler implementation preferred

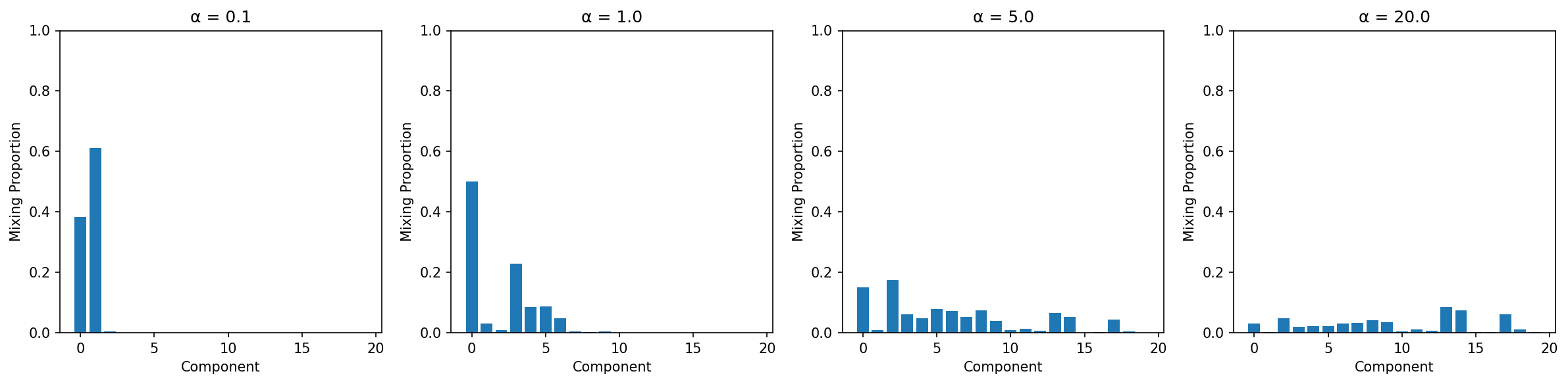
The Role of α (Concentration Parameter)

α controls the tendency to create new clusters:

1
2

# Try different alpha values
alphas = [0.1, 1.0, 5.0, 20.0]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

fig, axes = plt.subplots(1, 4, figsize=(16, 4))

for ax, alpha in zip(axes, alphas):
    # Generate stick-breaking weights
    key = random.PRNGKey(42)
    betas = []
    pis = []

    for k in range(20):  # Show first 20 components
        key, subkey = random.split(key)
        beta_k = jax.random.beta(subkey, 1.0, alpha)
        betas.append(beta_k)

        if k == 0:
            pi_k = beta_k
        else:
            pi_k = beta_k * (1.0 - sum(pis))
        pis.append(pi_k)

    # Plot
    ax.bar(range(20), pis)
    ax.set_xlabel('Component')
    ax.set_ylabel('Mixing Proportion')
    ax.set_title(f'α = {alpha}')
    ax.set_ylim([0, 1])

plt.tight_layout()
plt.savefig('stick_breaking_alpha.png', dpi=150, bbox_inches='tight')
plt.show()

Interpretation:

• α = 0.1: First component dominates (few clusters)
• α = 1.0: Moderate spread (balanced)
• α = 5.0: More components active (many clusters)
• α = 20.0: Very even spread (diffuse)

Real-World Applications

Anomaly Detection

• Normal data forms clusters
• Outliers create singleton clusters
• α controls sensitivity to outliers

Topic Modeling

• Documents are mixtures over topics
• DPMM discovers number of topics automatically
• Each topic is a distribution over words

Genomics

• Cluster genes by expression patterns
• Number of functional groups unknown
• DPMM identifies distinct expression profiles

Image Segmentation

• Pixels cluster by color/texture
• DPMM finds natural segments
• No need to specify number of segments

Practice Problems

Problem 1: Adjusting α

Using the observed bento data from earlier, run inference with α ∈ {0.5, 2.0, 10.0}.

a) How does the number of active clusters change?

b) How does posterior uncertainty change?

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

for alpha in [0.5, 2.0, 10.0]:
    # Update ALPHA global or pass as parameter
    print(f"\n=== Alpha = {alpha} ===")

    # Run inference (simplified for brevity)
    # traces = infer_dpmm(observed_weights, num_particles=500)

    # Count active clusters
    # active = count_active_clusters(traces)
    # print(f"Active clusters: {active}")

Problem 2: Sequential Learning

Chibany receives bentos one at a time. Implement online learning where the model updates as each bento arrives.

Hint: Use sequential importance resampling, updating the posterior after each observation.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

def online_dpmm(data_stream):
    """
    Learn DPMM parameters sequentially as data arrives
    """
    traces = []  # Posterior samples

    for i, x_new in enumerate(data_stream):
        print(f"Observation {i+1}: x = {x_new:.2f}")

        # Create constraints for all data seen so far
        constraints = choice_map()
        for j in range(i+1):
            constraints[f"x_{j}"] = data_stream[j]

        # Update posterior
        key, subkey = random.split(key)
        trace, _ = importance_resampling(dpmm_model, (i+1,), constraints, 100)(subkey)
        traces.append(trace)

        # Report discovered clusters
        mus = [trace[f"mu_{k}"] for k in range(KMAX)]
        active = [k for k, mu in enumerate(mus) if abs(mu) < 20]  # Heuristic
        print(f"  Active clusters: {active}")

    return traces

# Apply to bento stream
traces = online_dpmm(observed_weights)

What We’ve Accomplished

We started with a mystery: bentos with an average weight that doesn’t match any individual bento. Through this tutorial, we:

1. Chapter 1: Understood expected value paradoxes in mixtures
2. Chapter 2: Learned continuous probability (PDFs, CDFs)
3. Chapter 3: Mastered the Gaussian distribution
4. Chapter 4: Performed Bayesian learning for parameters
5. Chapter 5: Built Gaussian Mixture Models with EM
6. Chapter 6: Extended to infinite mixtures with DPMM

You now have the tools to:

• Model complex, multimodal data
• Discover latent structure automatically
• Quantify uncertainty in clustering
• Perform Bayesian inference with GenJAX

Further Reading

Theoretical Foundations

• Ferguson (1973): “A Bayesian Analysis of Some Nonparametric Problems” (original DP paper)
• Teh et al. (2006): “Hierarchical Dirichlet Processes” (extensions to HDP)
• Austerweil, Gershman, Tenenbaum, & Griffiths (2015): “Structure and Flexibility in Bayesian Models of Cognition” (Chapter in The Oxford Handbook of Computational and Mathematical Psychology - comprehensive overview of Bayesian nonparametric approaches to cognitive modeling)

Practical Implementations

• Neal (2000): “Markov Chain Sampling Methods for Dirichlet Process Mixture Models” (MCMC inference)
• Blei & Jordan (2006): “Variational Inference for Dirichlet Process Mixtures” (scalable inference)

GenJAX Documentation

• GenJAX GitHub - Official repository
• Probabilistic Programming Examples - Gen.jl (sister project)

Interactive Exploration

Want to experiment with DPMMs yourself? Try our interactive Jupyter notebook that lets you:

• Adjust the concentration parameter α and see its effect on clustering
• Add or remove data points and watch the model adapt
• Change the truncation level K_max
• Visualize posterior distributions in real-time

The notebook includes:

• Complete DPMM implementation with stick-breaking
• Interactive widgets for all parameters
• Real-time visualization of posteriors
• Guided exercises to deepen understanding

This is a great way to build intuition for how α, K_max, and the data itself interact to produce the posterior distribution.

Congratulations!

You’ve completed the tutorial on Continuous Probability and Bayesian Learning with GenJAX!

You’re now equipped to:

• Build probabilistic models for continuous data
• Perform Bayesian inference and learning
• Discover latent structure in data
• Use GenJAX for sophisticated probabilistic programming

Where to go next:

• Explore hierarchical models (Bayesian neural networks, hierarchical Bayes)
• Learn advanced inference (Hamiltonian Monte Carlo, variational inference)
• Apply to your own data (clustering, time series, causal inference)

Happy modeling! 🎉